Passo a passo para cálculo de REAÇÕES DE APOIO
O primeiro passo de um exercício na engenharia de estruturas será o cálculo das reações de apoio. As reações de apoio são chamadas também de forças externas REATIVAS. Com esse nome talvez seja mais fácil de entender o que elas significam. Então, vamos ver esse exemplo clássico de uma pessoa empurrando uma parede:

Conseguimos compreender que, quando nós empurramos a parede, ela precisa “nos empurrar de volta”, com uma força de mesma magnitude e direção, mas sentido oposto, para que nós fiquemos em equilíbrio.
Isso foi expresso na Terceira Lei ne Newton: “a toda ação corresponde a uma reação de igual intensidade, mas que atua no sentido oposto”
Nas estruturas, para que elas estejam em equilíbrio, precisamos fixa-las em alguns pontos (arbitrariamente escolhidos pelo projetista, dentro de certos parâmetros) e, nesses pontos, teremos APOIOS (igual o seu pé é um apoio para o seu corpo)…
Ainda não acabou não…. Só pra dar uma descontraída rsrs
Voltando ao nosso assunto. Pois bem, as cargas externas aplicadas na sua estrutura se deslocarão por ela até encontrar os apoios, onde serão encaminhadas ao solo pelas fundações. Nesses APOIOS, aparecerão REAÇÕES (Terceira Lei de Newton), que chamamos então de REAÇÕES DE APOIO.
Vai aí um passo a passo para você seguir sempre que for calcular suas reações de apoio:
- Identificar os tipos de apoio que existem na sua estrutura (se do 1⁰, 2⁰ ou 3⁰ gênero);
- Desenhar o diagrama de corpo livre da sua estrutura (representação daquilo que é essencial para resolver o problema)
- Aplicar as equações de equilíbrio da estática (no plano ou no espaço).
Seguindo sempre esse passo a passo, você vai conseguir desenvolver o seu exercício com mais facilidade.
Caso você queira assistir uma resolução de cálculo de reação de apoio em vigas, seguindo os 3 passos acima apresentados, é só assistir esse vídeo:
Lá no canal você pode encontrar outros vídeos sobre Estática, Resistência dos Materiais e Mecânica das Estruturas.
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Telegram: https://t.me/profcarolgrossi/
Um abraço, fiquem com Deus e até mais!
O que são treliças COMPOSTAS e COMPLEXAS?
As treliças podem ser classificadas de acordo com sua formação em treliças simples, compostas e complexas. No artigo da semana passada nós falamos sobre as treliças simples e hoje vamos fechar esse assunto falando um pouco sobre as treliças compostas e as treliças complexas.
Só para contextualizar, a treliça simples é aquela que segue a lei de formação das treliças, iniciando num módulo triangular ABC e acrescentando duas barras para cada nó. Mas, nem toda treliça segue esse padrão de formação. Esse é o caso das treliças compostas e das treliças complexas. Então vamos entender agora esses dois casos.
A treliça composta é formada conectando duas ou mais treliças simples. É bastante frequente utilizar esse tipo de treliça, já que ela consegue vencer vãos maiores e formando uma estrutura mais leve do que se utilizássemos uma única treliça simples.
Existem 3 maneiras que podemos usar para juntar as treliças simples em uma composta:
– As treliças podem ser ligadas por um nó e uma barra em comum

– As treliças podem ser combinadas por três barras

– As treliças podem ser combinadas de modo que barras de uma treliça simples grande, chamada de treliça principal, sejam substituídas por treliças simples chamadas de treliças secundárias.

Já em relação às treliças complexas é uma treliça que não é nem simples, nem composta. Ponto final. É, pra essa aqui não tem muito o que se falar. Vamos ver dois exemplo de treliça complexa:

Caso você queira ver esse conteúdo em vídeo, te recomendo ir nesse vídeo aqui, que está no meu canal do YouTube.
Lá no canal você pode encontrar outros vídeos sobre Estática, Resistência dos Materiais e Mecânica das Estruturas.
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Telegram: https://t.me/profcarolgrossi/
Um abraço, fiquem com Deus e até mais!
Como são formadas as TRELIÇAS SIMPLES?
No artigo de hoje mós vamos de uma forma rápida qual é o princípio de formação de uma treliça simples
Voce sabe quais são as duas simplificações de projeto que existem quando falamos de treliças? Esse será o nosso assunto hoje, nós vamos entender os principais aspectos das treliças planas e as simplificações que utilizamos em projeto.
No último artigo nós conversamos sobre as duas hipóteses de projeto que precisamos considerar ao calcularmos treliças. Se vocês se lembram, uma dessas hipóteses diz que os nós são considerados rótulas perfeitas (os nós são os encontros das barras). Além disso, nossa treliça é formada por triângulos (geometricamente estável).
Para formar um triângulo eu preciso de três peças. Se os três membros são conectados por pinos em suas extremidades, eles formam uma peça que chamamos de unidade básica triangular, que será geometricamente estável

Agora, se temos um retângulo ligado por nós rotulados, não conseguimos a mesma coisa:
E, se acrescentarmos uma barra de modo a criar dois triângulos, voltamos a ter uma peça estável.
Agora que já entendemos o porquê das treliças serem formadas por triângulos, vamos seguir adiante. Como, então, formamos uma treliça simples? Unindo dois ou mais membros e conectá-los a um novo nó D forma uma treliça maior. Esse procedimento pode ser repetido tantas vezes quanto desejado para formar uma treliça ainda maior.
Concluindo, se uma treliça pode ser formada expandindo a treliça básica triangular dessa forma (um nó + duas barras), ela é chamada de treliça simples.
Vamos ver dois exemplos pra fechar:

a. Nó D com acréscimo das barras BD, CD
b. Nó E com acréscimo das barras CE, DE

a. Nó D com acréscimo das barras AD, CD
b. Nó E com acréscimo das barras CE, BE
c. Nó F com acréscimo das barras BF, EF
d. Nó G com acréscimo das barras EG, FG
e. Nó H com acréscimo das barras FH, GH
Caso você queira ver esse conteúdo em vídeo, te recomendo ir nesse vídeo aqui, que está no meu canal do YouTube.
Lá no canal você pode encontrar outros vídeos sobre Estática, Resistência dos Materiais e Mecânica das Estruturas.
No artigo da semana que vem nós vamos ver sobre as treliças classificadas como compostas e complexas: LINK A SER LIBERADO DIA 19/07
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Telegram: https://t.me/profcarolgrossi/
Um abraço, fiquem com Deus e até mais!
HIPÓTESES de cálculo de TRELIÇAS, você sabe quais são?
Se você está lendo esse artigo é porque está interessado em aprender como se calcula uma treliça, não é mesmo? Se você seguir meu passo a passo, percorrendo todos os textos e vídeos eu tenho CERTEZA que você não vai errar mais nenhum cálculo de treliça. Então vamos lá!
Voce sabe quais são as duas simplificações de projeto que existem quando falamos de treliças? Esse será o nosso assunto hoje, nós vamos entender os principais aspectos das treliças planas e as simplificações que utilizamos em projeto.
As treliças são estruturas com membros esbeltos (alongados, delgados) e conectados entre si em suas extremidades. Os membros são geralmente de madeira ou aço. Nesse vídeo vamos nos concentrar nas treliças planas, ou seja, a treliça pode ser estudada no plano xy e possui cargas atuantes também no plano xy.
O que a gente terá sempre que pensar? A força resultante se calcula pela ÁREA DO CARREGAMENTO e ponto de aplicação se dá no CENTROIDE DESSA ÁREA
As treliças são muito encontradas para suportar telhados:

e pontes

Mas, todo elemento pode ser feito maciço ou treliçado, como por exemplo:
– Pilares treliçados

– Pórticos treliçados

Vamos analisar essa estrutura aqui, um exemplo típico de treliças de telhado [Estática Mecânica para Engenharia 14ª edição Hibbeler].

Se observamos, a carga do telhado é transmitida para a treliça nos nós através das terças, e podemos desenhar um rascunho da treliça da seguinte maneira:

Agora, vamos analisar essa estrutura aqui, uma treliça de ponte.

Aqui, o peso no leito é transmitido primeiro para as longarinas, depois para as vigas de piso que, finalmente, descarregam nos nós das duas treliças de suporte, como mostra o rascunho abaixo:

Existe uma semelhança na aplicação da carga externa nos dois exemplos mostrados, que constitui a nossa PRIMEIRA HIPÓTESE DE PROJETO.
1° – Todas as cargas são aplicadas nos nós. É muito importante que essa hipótese de projeto seja mantida na vida real. Treliças com as condições apresentadas abaixo podem gerar problemas futuros. As barras são esbeltas e podem não suportar de forma eficiente a carga.


Se vocês notarem, nos dois rascunhos (esquemas das treliças) existe uma bolinha ali no encontro das barras, correto? Sim, essa é a nossa SEGUNDA HIPÓTESE DE PROJETO.
2° – As barras são conectadas entre si por rótulas perfeitas. As barras são livres para rotacionar em torno do eixo z e, com isso, não absorvem nenhum momento.
Em razão dessas duas hipóteses, cada membro da treliça agirá como um membro de duas forças e a força atuando em cada extremidade do membro será direcionada ao longo do seu eixo.
Se a força tender a alongar o membro, ela será uma força de TRAÇÃO (T); Se a força tende a encurtar o membro, ela será uma força de COMPRESSÃO (C)


Nosso objetivo ao resolver o projeto de uma treliça é encontrar a magnitude da força normal que atua na barra e se ela é de tração ou de compressão. AQUI O SINAL IMPORTA MUITO. O comportamento de barras tracionadas é bem menos complexo do que o comportamento de barras comprimidas, que podem sofrer um fenômeno que chamamos de flambagem (colocar imagem fazendo a flambagem com a régua).
É, infelizmente aqui aquela famosa pergunta: mas professora, eu errei só o sinal. Vou perder a questão inteira? Possui uma resposta nada agradável de “sim, errou o sinal da treliça, errou foi tudo”.
Caso você queira ver esse conteúdo em vídeo, te recomendo ir nesse vídeo aqui, que está no meu canal do YouTube.
Lá no canal você pode encontrar outros vídeos sobre Estática, Resistência dos Materiais e Mecânica das Estruturas.
Agora que você já sabe as duas hipóteses de projeto necessárias para estabelecimento do problema de uma treliça, vamos aprender a calcular as normais nas barras? Temos dois métodos (método dos nós e método das seções).
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Telegram: https://t.me/profcarolgrossi/
Um abraço, fiquem com Deus e até mais!
Resultante de carregamento distribuído: uniforme e triangular
No último artigo nós aprendemos o que representam os carregamentos que utilizamos nas matérias da engenharia de estruturas (Estática, Mecânica das Estruturas e Mecânica dos Sólidos) na vida real. Vimos um pouco sobre carregamento concentrado, carregamento distribuído uniformemente e carregamento distribuído linearmente (triangular).
Agora, nesse artigo, nós vamos aprender como calcular a resultante dos carregamentos distribuídos e como encontrar o ponto de atuação. Primeiramente nós vamos fazer uma forma BEM SIMPLES, que é a forma que vocês utilizarão nos exercícios.
Num próximo momento, eu vou mostrar de onde veio essa forma simples, pra quem quiser se aprofundar um pouco mais no assunto. Então vamos lá?
O que a gente terá sempre que pensar? A força resultante se calcula pela ÁREA DO CARREGAMENTO e ponto de aplicação se dá no CENTROIDE DESSA ÁREA
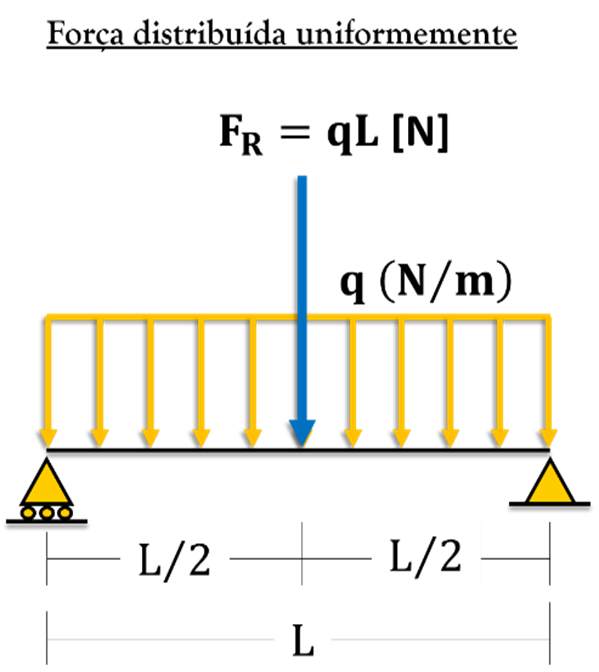
- O primeiro carregamento distribuído que nós vamos resolver será o carregamento uniforme

Como podemos perceber, a área do carregamento é retangular. Então, pra calcular a resultante é só multiplicar o valor da altura do retângulo: valor do carregamento – q (N/m) pelo comprimento do retângulo: dimensão onde o carregamento atua – L (m). Então, teremos:
1. Se essa área for pequena em comparação com a área da superfície total do corpo, então podemos IDEALIZAR essa superfície como uma FORÇA CONCENTRADA (medida em N) aplicada a UM PONTO.
Um exemplo de força concentrada é a força descarregada pelos pilares nas fundações. Ou as forças descarregadas pelas vigas nos pilares. Ou uma força de um cabo na extremidade de uma estrutura

Essa resultante estará aplicada no centroide do retângulo e sabemos que esse ponto fica exatamente no meio do seu comprimento. Logo, nossa força resultante ficará assim:
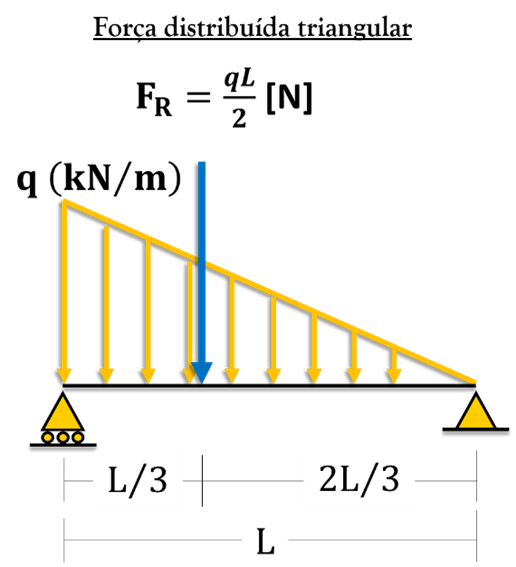
2. Carregamento com variação linear (triangulo)

Como podemos perceber, a área do carregamento é triangular. Então, paraa calcular a resultante basta multiplicar o valor da altura do triângulo (valor do carregamento) pelo comprimento do triângulo (dimensão que ele atua) e dividir por dois. Então, teremos:

Essa resultante estará aplicada no centroide do triângulo, e sabemos que esse ponto fica localizado a L/3 da base do triângulo e 2L/3 da ponta do triângulo. Logo, nossa força resultante ficará assim:
3. Carregamento do tipo trapézio

O que acontece aqui é que temos uma junção de retângulo com triângulo. Podemos separar essas duas figuras e calcular duas resultantes (uma para o triângulo e outra para o retângulo). O que precisamos estar muito atentos é na definição correta das alturas das figuras.

Se a altura total é 10 kN/m e a altura do lado menor do trapézio é 3 kN/m teremos:
Retângulo com altura de 3 kN/m e triângulo com altura de (10 kN/m – 3 kN/m = 7 kN/m). E aí é só proceder como foi mostrado anteriormente.
Vamos fazer no próximo artigo alguns exercícios de aplicação que aparecem nos exemplos da Estática, RM e MecEstr?
Aproveite para reforçar esse conhecimento assistindo a vídeo aula desse tema no meu canal do Youtube:
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Telegram: https://t.me/profcarolgrossi/
Um abraço, fiquem com Deus e até mais!
Cargas reais da estática: o que você está calculando?
Vamos conseguir identificar na vida real os carregamentos que utilizamos nos exercícios das disciplinas da Estruturas? Nas disciplinas de Estática, Mecânica dos Sólidos (ou Resistência dos Materiais) e Mecânica das Estruturas, além das disciplinas específicas como Concreto, Aço e Madeira, nós sempre usamos um tanto de seta… Seta sozinha, seta em grupo, seta com tamanho diferente. Não é mesmo? Vamos entender o que são essas setas (forças) e onde elas aparecem na vida real.
No artigo de hoje nós vamos falar sobre as forças que corpos exercem um sobre os outros.
E não, eu não vou entrar em conceitos abstratos, vamos direto ao ponto.
O que é força?
Temos 2 tipos de força externa que podem atuar nas nossas estruturas: forças de superfície e forças de corpo.
As forças de superfície são causadas pelo contato direto de um corpo com a superfície do outro (ação e reação: se eu empurro a mesa, eu exerço uma força na mesa e ela me empurra de volta com a mesma magnitude) Em todos os casos, essas forças estão distribuídas sobre uma área de contato entre os corpos.
1. Se essa área for pequena em comparação com a área da superfície total do corpo, então podemos IDEALIZAR essa superfície como uma FORÇA CONCENTRADA (medida em N) aplicada a UM PONTO.
Um exemplo de força concentrada é a força descarregada pelos pilares nas fundações. Ou as forças descarregadas pelas vigas nos pilares. Ou uma força de um cabo na extremidade de uma estrutura
2. Se a força de superfície for aplicada ao longo de uma área estreita, ela pode ser IDEALIZADA como uma carga distribuída linear, q(x). Nesse caso, a força é medida em N/m, representada por uma série de setas ao longo do eixo x da estrutura.
Um exemplo de força distribuída é a força que uma parede descarrega numa viga. Essa força pode ser uniforme ou pode ter algum outro tipo de distribuição (triangular, trapezoidal, etc).
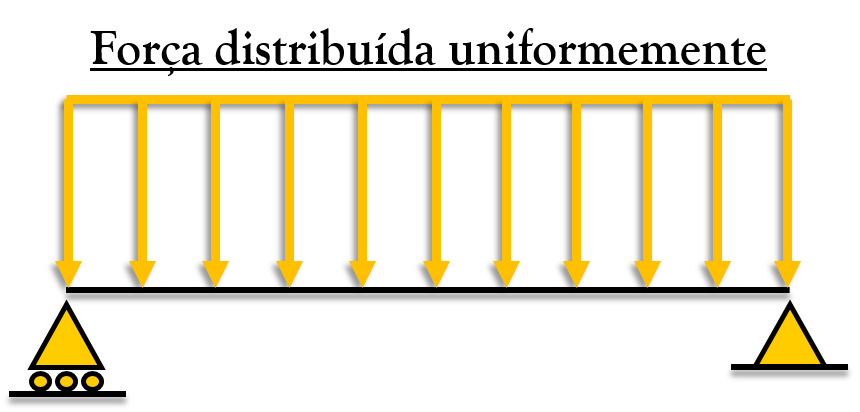

A força de corpo é desenvolvida quando um corpo exerce força sobre o outro, sem contato físico direto entre eles. Por exemplo, a força da gravidade atuando em todos os corpos. Iremos achar essa força a partir do peso próprio dos elementos que formam a nossa estrutura.
Agora na prática, o que acontece?
Quando pegamos um problema físico e decidimos analisa-lo matematicamente, temos que representar o que está acontecendo na vida real da maneira mais próxima possível. Então vamos ver como essas forças são representadas nos nossos problemas de Estática:
Forças de superfície: modela o formado das forças externas à estrutura
1. Idealizada como uma força concentrada
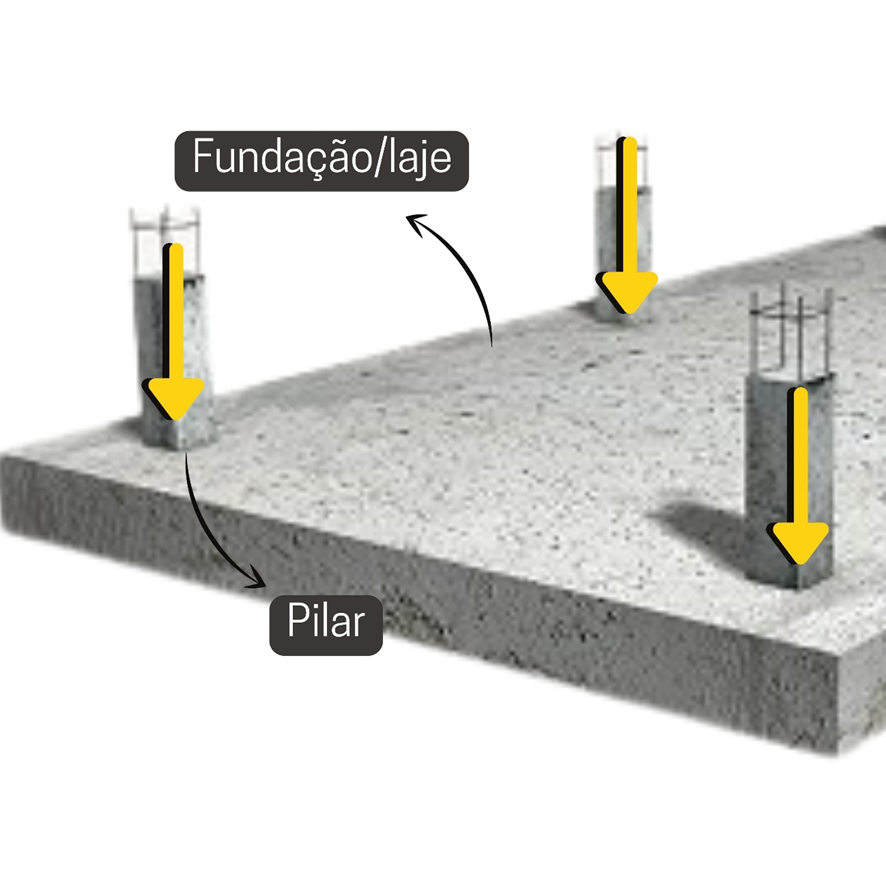
Imagem 01: Pilares descarregando em uma fundação do tipo radier
Cabo sendo puxado na ponta de uma viga
2. Idealizada como uma carga distribuída

Figura 02: Parede descarregando em uma viga de forma uniforme

Figura 03 Parede de cobertura descarregando em uma viga em formato linear (triângulo)
Força de corpo: modela o peso próprio das estruturas
E aí, você sabe como calcular a força resultante de carregamentos distribuídos? E localizar o ponto de atuação? E mais ainda, para o que servem esses cálculos? Vamos dar sequência nesse assunto no próximo artigo! Só clicar aqui.
Aproveite para reforçar esse conhecimento assistindo a vídeo aula desse tema no meu canal do Youtube: https://www.youtube.com/channel/UC1QPciddN2N5RPJ18PpQPzw
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Um abraço, fiquem com Deus e até mais!