No último artigo nós aprendemos o que representam os carregamentos que utilizamos nas matérias da engenharia de estruturas (Estática, Mecânica das Estruturas e Mecânica dos Sólidos) na vida real. Vimos um pouco sobre carregamento concentrado, carregamento distribuído uniformemente e carregamento distribuído linearmente (triangular).
Agora, nesse artigo, nós vamos aprender como calcular a resultante dos carregamentos distribuídos e como encontrar o ponto de atuação. Primeiramente nós vamos fazer uma forma BEM SIMPLES, que é a forma que vocês utilizarão nos exercícios.
Num próximo momento, eu vou mostrar de onde veio essa forma simples, pra quem quiser se aprofundar um pouco mais no assunto. Então vamos lá?
O que a gente terá sempre que pensar? A força resultante se calcula pela ÁREA DO CARREGAMENTO e ponto de aplicação se dá no CENTROIDE DESSA ÁREA
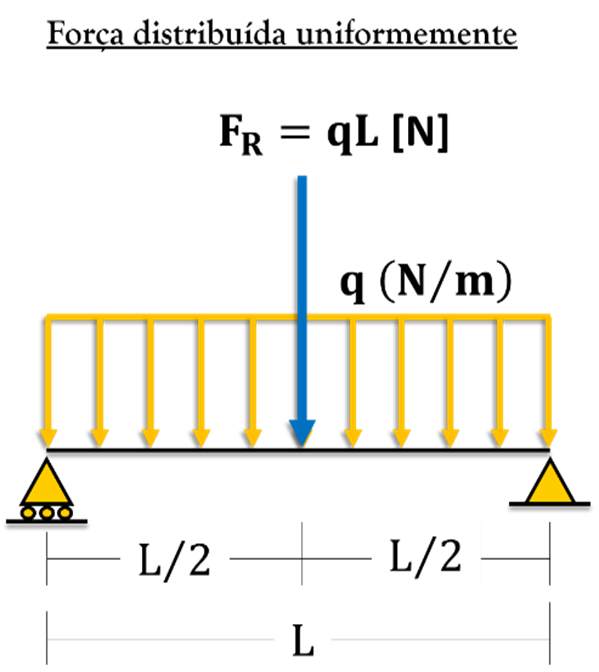
- O primeiro carregamento distribuído que nós vamos resolver será o carregamento uniforme

Como podemos perceber, a área do carregamento é retangular. Então, pra calcular a resultante é só multiplicar o valor da altura do retângulo: valor do carregamento – q (N/m) pelo comprimento do retângulo: dimensão onde o carregamento atua – L (m). Então, teremos:
1. Se essa área for pequena em comparação com a área da superfície total do corpo, então podemos IDEALIZAR essa superfície como uma FORÇA CONCENTRADA (medida em N) aplicada a UM PONTO.
Um exemplo de força concentrada é a força descarregada pelos pilares nas fundações. Ou as forças descarregadas pelas vigas nos pilares. Ou uma força de um cabo na extremidade de uma estrutura

Essa resultante estará aplicada no centroide do retângulo e sabemos que esse ponto fica exatamente no meio do seu comprimento. Logo, nossa força resultante ficará assim:
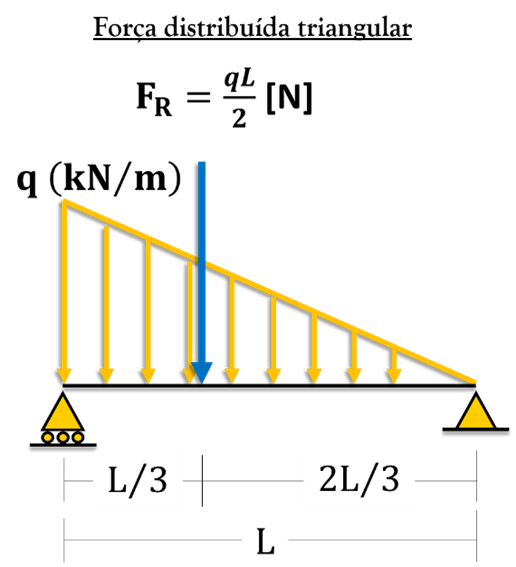
2. Carregamento com variação linear (triangulo)

Como podemos perceber, a área do carregamento é triangular. Então, paraa calcular a resultante basta multiplicar o valor da altura do triângulo (valor do carregamento) pelo comprimento do triângulo (dimensão que ele atua) e dividir por dois. Então, teremos:

Essa resultante estará aplicada no centroide do triângulo, e sabemos que esse ponto fica localizado a L/3 da base do triângulo e 2L/3 da ponta do triângulo. Logo, nossa força resultante ficará assim:
3. Carregamento do tipo trapézio

O que acontece aqui é que temos uma junção de retângulo com triângulo. Podemos separar essas duas figuras e calcular duas resultantes (uma para o triângulo e outra para o retângulo). O que precisamos estar muito atentos é na definição correta das alturas das figuras.

Se a altura total é 10 kN/m e a altura do lado menor do trapézio é 3 kN/m teremos:
Retângulo com altura de 3 kN/m e triângulo com altura de (10 kN/m – 3 kN/m = 7 kN/m). E aí é só proceder como foi mostrado anteriormente.
Vamos fazer no próximo artigo alguns exercícios de aplicação que aparecem nos exemplos da Estática, RM e MecEstr?
Aproveite para reforçar esse conhecimento assistindo a vídeo aula desse tema no meu canal do Youtube:
Qualquer dúvida, só comentar aqui embaixo.
Você também consegue me achar nas redes sociais:
Facebook: https://www.facebook.com/prof.carolgrossi
Instagram: https://www.instagram.com/carollgrossi/
Telegram: https://t.me/profcarolgrossi/
Um abraço, fiquem com Deus e até mais!